机器学习----支持向量机

第三章

第五部分 支持向量机(Support Vector Machines)

本章的讲义主要讲述的是 支持向量机（Support Vector Machine ，缩写为 SVM） 学习算法。SVM 算得上是现有的最好的现成的(“off-the-shelf”)监督学习算法之一，很多人实际上认为这里没有“之一”这两个字的必要，认为 SVM 就是最好的现成的监督学习算法。讲这个 SVM 的来龙去脉之前，我们需要先讲一些关于边界的内容，以及对数据进行分割成大的区块（gap）的思路。接下来，我们要讲一下最优边界分类器(optimal margin classifier,)，其中还会引入一些关于拉格朗日对偶(Lagrange duality)的内容。然后我们还会接触到核(Kernels)，这提供了一种在非常高的维度(例如无穷维度)中进行 SVM 学习的高效率方法，最终本章结尾部分会讲 SMO 算法，也就是 SVM 算法的一个有效实现方法。

1 边界(Margins)：直觉(Intuition)

咱们这回讲 SVM 学习算法，从边界(margins)开始说起。这一节我们会给出关于边界的一些直观展示(intuitions)，以及对于我们做出的预测的信心(confidence)；在本章的第三节中，会对这些概念进行更正式化的表述。

考虑逻辑回归，其中的概率分布\(p(y = 1|x;\theta)\) 是基于 \(h_\theta(x) = g(\theta^Tx)\) 而建立的模型。当且仅当 \(h_\theta(x) \geq 0.5\) ，也就是 \(\theta^Tx \geq 0\) 的时候，我们才会预测出“\(1\)”。假如有一个正向(Positive)的训练样本(positive tra_ining example)(\(y = 1\))。那么\(\theta^Tx\) 越大，\(h_\theta (x) = p(y = 1|x; w, b)\) 也就越大，我们对预测 Label 为 \(1\) 的“信心(confidence)”也就越强。所以如果 \(y = 1\) 且 \(\theta^T x \gg 0\)（远大于 \(0\)），那么我们就对这时候进行的预测非常有信心，当然这只是一种很不正式的粗略认识。与之类似，在逻辑回归中，如果有 \(y = 0\) 且 \(\theta^T x \ll 0\)(远小于 0)，我们也对这时候给出的预测很有信心。所以还是以一种非常不正式的方式来说，对于一个给定的训练集，如果我们能找到一个 \(\theta\)，满足当 \(y^{(i)} = 1\) 的时候总有 \(\theta^T x^{(i)} \gg 0\)，而 \(y^{(i)} = 0\) 的时候则 \(\theta^T x^{(i)} \ll 0\)，我们就说这个对训练数据的拟合很好，因为这就能对所有训练样本给出可靠（甚至正确）的分类。似乎这样就是咱们要实现的目标了，稍后我们就要使用函数边界记号(notion of functional margins) 来用正规的语言来表达该思路。

还有另外一种的直观表示，例如下面这个图当中，画叉的点表示的是正向训练样本，而小圆圈的点表示的是负向训练样本，图中还画出了分类边界(decision boundary)， 这条线也就是通过等式 \(\theta^T x = 0\) 来确定的，也叫做分类超平面(separating hyperplane)。 图中还标出了三个点 \(A，B 和 C\)。

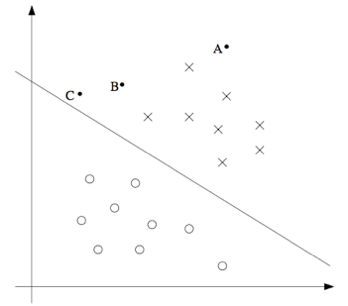
可以发现 \(A\) 点距离分界线很远。如果我们对 \(A\) 点的 \(y\) 值进行预测，估计我们会很有信心地认为在那个位置的 \(y = 1\)。与之相反的是 \(C\)，这个点距离边界线很近，而且虽然这个 \(C\) 点也在预测值 \(y = 1\) 的一侧，但看上去距离边界线的距离实在是很近的，所以也很可能会让我们对这个点的预测为 \(y = 0\)。因此，我们对 \(A\) 点的预测要比对 \(C\) 点的预测更有把握得多。\(B\) 点正好在上面两种极端情况之间，更广泛地说，如果一个点距离分类超平面(separating hyperplane) 比较远，我们就可以对给出的预测很有信心。那么给定一个训练集，如果我们能够找到一个分类边界，利用这个边界我们可以对所有的训练样本给出正确并且有信心（也就是数据点距离分类边界要都很远）的预测，那这就是我们想要达到的状态了。当然上面这种说法还是很不正规，后面我们会使用几何边界记号(notion of geometric margins) 来更正规地来表达。

2 记号(Notation)

在讨论 SVMs 的时候，出于简化的目的，我们先要引入一个新的记号，用来表示分类。假设我们要针对一个二值化分类的问题建立一个线性分类器，其中用来分类的标签(label)为 \(y\)，分类特征(feature)为 \(x\)。从此以后我们就用 $y