LDA

LDA 原理

给定数据\(\mathbf{X}\in \mathbb{R}^{N\times p}\)，以及\(\mathbf{y}\in \{0,1\}\)，构成输入与输出训练数据对\(D=\{(\mathbf{x}_1,\mathbf{y}_1),...,(\mathbf{x}_N,\mathbf{y}_N)\}\)。训练集\(D\)表示整个训练数据集有\(N\)条数据，每一条数据的维度为\(p\)维，所有数据只有两个类别分别对应于输出\(\mathbf{y}\)取值为0或者1。

首先假设两类数据中第一类数据\(\mathbf{x}_{c1}\)有\(|\mathbf{x}_{c1}|=N_1\)个，第二类数据有\(|\mathbf{x}_{c2}|=N_2\)个，且\(N_1+N_2=N\)。两类数据的均值和方差可以表示为：

\[ \bar{\mathbf{x_1}}=\frac{1}{N_1}\sum_{i=1}^{N_1}\mathbf{x}_i \]

\[ \bar{\mathbf{x_2}}=\frac{1}{N_2}\sum_{i=1}^{N_2}\mathbf{x}_i \]

\[ \mathbf{S}_{x1}=\frac{1}{N_1}\sum_{i=1}^{N_1}(\mathbf{x}_i-\bar{\mathbf{x_1}})(\mathbf{x}_i-\bar{\mathbf{x_1}})^T \]

\[ \mathbf{S}_{x2}=\frac{1}{N_2}\sum_{i=1}^{N_2}(\mathbf{x}_i-\bar{\mathbf{x_2}})(\mathbf{x}_i-\bar{\mathbf{x_2}})^T \]

对输入的\(p\)维特征进行降维有\(\mathbf{z}_i=\mathbf{W}^T\mathbf{x}_i\)，其中\(\mathbf{z}\)表示降维之后的数据，那么降维之后的数据的均值和方差分别为：

\[ \bar{\mathbf{z_1}}=\frac{1}{N_1}\sum_{i=1}^{N_1}\mathbf{W}^T\mathbf{x}_i \]

\[ \mathbf{S}_1=\frac{1}{N_1}\sum_{i=1}^{N_1}(\mathbf{W}^T\mathbf{x}_i-\bar{\mathbf{z_1}})(\mathbf{W}^T\mathbf{x}_i-\bar{\mathbf{z_1}})^T \]

\[ \bar{\mathbf{z_2}}=\frac{1}{N_2}\sum_{i=1}^{N_2}\mathbf{W}^T\mathbf{x}_i \]

\[ \mathbf{S}_2=\frac{1}{N_2}\sum_{i=1}^{N_2}(\mathbf{W}^T\mathbf{x}_i-\bar{\mathbf{z_2}})(\mathbf{W}^T\mathbf{x}_i-\bar{\mathbf{z_2}})^T \]

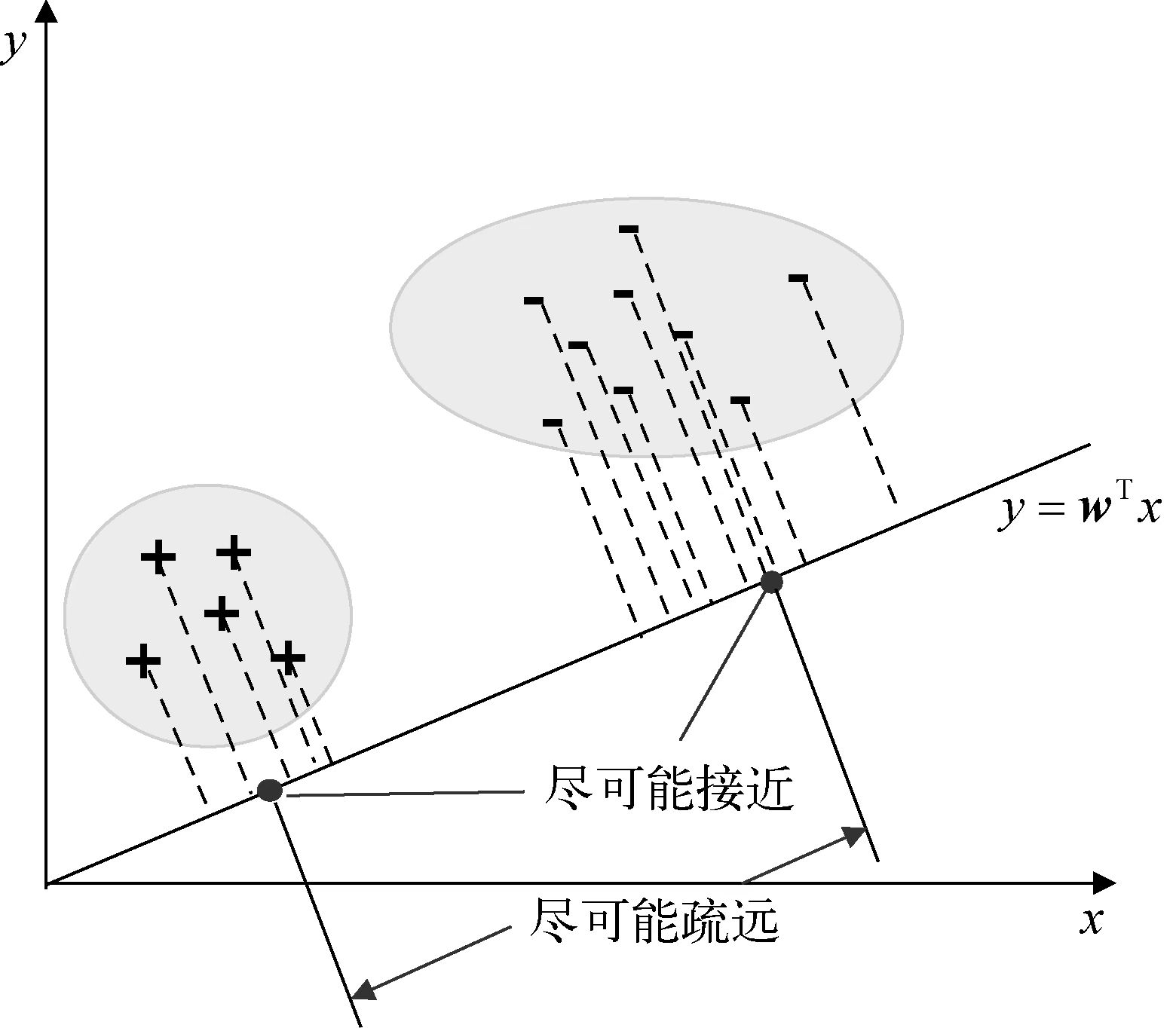LDA的示意图如上图所示，它的最终目的是使得同一类型的数据之间尽可能地聚集在一起，使得位于不同类别的两类数据尽可能分开。首先是让位于同一类别的数据尽可能地聚集在一起，实际上就是让两类数据的方差尽可能小\(\min \mathbf{S}_1+\mathbf{S}_2\)。其次是让位于不同类别的数据之间尽可能离得远，这一点可以通过让两类数据的中心也就是均值之间的距离尽可能远\(\max|| \bar{\mathbf{z}_1}-\bar{\mathbf{z}_2}||_F^2\) 最终LDA的目标函数可以表示为：

\[ L = \frac{|| \bar{\mathbf{z}_1}-\bar{\mathbf{z}_2}||_F^2}{\mathbf{S}_1+\mathbf{S}_2} \]

首先对分子进行化简有：

\[ \begin{aligned} || \bar{\mathbf{z}_1}-\bar{\mathbf{z}_2}||_F^2&=||\frac{1}{N_1}\sum_{x=1}^{N_1}\mathbf{W}^T\mathbf{x}_i-\frac{1}{N_2}\sum_{x=1}^{N_2}\mathbf{W}^T\mathbf{x}_i||_F^2\\ &=||\mathbf{W}^T(\frac{1}{N_1}\sum_{t=1}^{N_1}\mathbf{x}_i-\frac{1}{N_2}\sum_{t=1}^{N_2}\mathbf{x}_i)||_F^2\\ &=||\mathbf{W}^T(\bar{\mathbf{x_1}}-\bar{\mathbf{x_2}})||_F^2\\ &=\mathbf{W}^T(\bar{\mathbf{x_1}}-\bar{\mathbf{x_2}})(\bar{\mathbf{x_1}}-\bar{\mathbf{x_2}})^T\mathbf{W} \end{aligned} \]

对分母进行化简有：

\[ \begin{aligned} \mathbf{S_1+S_2}&=\frac{1}{N_1}\sum_{i=1}^{N_1}(\mathbf{W}^T\mathbf{x}_i-\bar{\mathbf{z_1}})(\mathbf{W}^T\mathbf{x}_i-\bar{\mathbf{z_1}})^T+\frac{1}{N_2}\sum_{i=1}^{N_2}(\mathbf{W}^T\mathbf{x}_i-\bar{\mathbf{z_2}})(\mathbf{W}^T\mathbf{x}_i-\bar{\mathbf{z_2}})^T\\ &=\frac{1}{N_1}\sum_{i=1}^{N_1}(\mathbf{W}^T\mathbf{x}_i-\frac{1}{N_1}\sum_{i=1}^{N_1}\mathbf{W}^T\mathbf{x}_i)(\mathbf{W}^T\mathbf{x}_i-\frac{1}{N_1}\sum_{i=1}^{N_1}\mathbf{W}^T\mathbf{x}_i)^T\\ &+\frac{1}{N_2}\sum_{i=1}^{N_2}(\mathbf{W}^T\mathbf{x}_i-\frac{1}{N_2}\sum_{i=1}^{N_2}\mathbf{W}^T\mathbf{x}_i)(\mathbf{W}^T\mathbf{x}_i-\frac{1}{N_2}\sum_{i=1}^{N_2}\mathbf{W}^T\mathbf{x}_i)^T\\ &=\mathbf{W}^T\frac{1}{N_1}\sum_{i=1}^{N_1}(\mathbf{x}_i-\frac{1}{N_1}\sum_{i=1}^{N_1}\mathbf{x}_i)(\mathbf{x}_i-\frac{1}{N_1}\sum_{i=1}^{N_1}\mathbf{x}_i)^T\mathbf{W}\\ &=\mathbf{W}^T\frac{1}{N_2}\sum_{i=1}^{N_2}(\mathbf{x}_i-\frac{1}{N_2}\sum_{i=1}^{N_2}\mathbf{x}_i)(\mathbf{x}_i-\frac{1}{N_2}\sum_{i=1}^{N_2}\mathbf{x}_i)^T\mathbf{W}\\ &=\mathbf{W}^T\frac{1}{N_1}\sum_{i=1}^{N_1}(\mathbf{x}_i-\bar{\mathbf{x}_1})(\mathbf{x}_i-\bar{\mathbf{x}_1})^T\mathbf{W}+\mathbf{W}^T\frac{1}{N_2}\sum_{i=1}^{N_2}(\mathbf{x}_i-\bar{\mathbf{x}_2})(\mathbf{x}_i-\bar{\mathbf{x}_2})^T\mathbf{W}\\ &=\mathbf{W}^T(\mathbf{S}_{x1}-\mathbf{S}_{x2})\mathbf{W} \end{aligned} \]

最终LDA的目标函数可以表示为：

\[ L = \frac{\mathbf{W}^T(\bar{\mathbf{x_1}}-\bar{\mathbf{x_2}})(\bar{\mathbf{x_1}}-\bar{\mathbf{x_2}})^T\mathbf{W}}{\mathbf{W}^T(\mathbf{S}_{x1}-\mathbf{S}_{x2})\mathbf{W}} \]

令\(\mathbf{S}_{w}= (\bar{\mathbf{x_1}}-\bar{\mathbf{x_2}})(\bar{\mathbf{x_1}}-\bar{\mathbf{x_2}})^T\)，\(\mathbf{S}_{b}= \mathbf{S}_{x1}-\mathbf{S}_{x2}\)有：

\[ L = \frac{\mathbf{W}^T\mathbf{S}_w\mathbf{W}}{\mathbf{W}^T\mathbf{S}_b\mathbf{W}} \]

求解目标函数中的\(\mathbf{W}\)可以得到最终的解。

算法实现

import numpy as np

import matplotlib.pyplot as plt
import matplotlib.cm as cmx
import matplotlib.colors as colors
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

class LDA():
    def __init__(self):
        # 初始化权重矩阵
        self.w = None
    
    # 计算协方差矩阵
    def calc_cov(self, X, Y=None):
        m = X.shape[0]
        # 数据标准化
        X = (X - np.mean(X, axis=0))/np.std(X, axis=0)
        Y = X if Y == None else (Y - np.mean(Y, axis=0))/np.std(Y, axis=0)
        return 1 / m * np.matmul(X.T, Y)
  
    # 对数据进行投影
    def project(self, X, y):
        self.fit(X, y)
        X_projection = X.dot(self.w)
        return X_projection
  
    # LDA拟合过程
    def fit(self, X, y):
        # 按类分组
        X0 = X[y == 0]
        X1 = X[y == 1]

        # 分别计算两类数据自变量的协方差矩阵
        sigma0 = self.calc_cov(X0)
        sigma1 = self.calc_cov(X1)
        # 计算类内散度矩阵
        Sw = sigma0 + sigma1

        # 分别计算两类数据自变量的均值和差
        u0, u1 = np.mean(X0, axis=0), np.mean(X1, axis=0)
        mean_diff = np.atleast_1d(u0 - u1)

        # 对类内散度矩阵进行奇异值分解
        U, S, V = np.linalg.svd(Sw)
        # 计算类内散度矩阵的逆
        Sw_ = np.dot(np.dot(V.T, np.linalg.pinv(np.diag(S))), U.T)
        # 计算w
        self.w = Sw_.dot(mean_diff)

  
    # LDA分类预测
    def predict(self, X):
        y_pred = []
        for sample in X:
            h = sample.dot(self.w)
            y = 1 * (h < 0)
            y_pred.append(y)
        return y_pred


data = datasets.load_iris()
X = data.data
y = data.target

X = X[y != 2]
y = y[y != 2]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=41)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

lda = LDA()
lda.fit(X_train, y_train)
y_pred = lda.predict(X_test)

from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_pred)
print(accuracy)

def calculate_covariance_matrix(X, Y=None):
    if Y is None:
        Y = X
    n_samples = np.shape(X)[0]
    covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))

    return np.array(covariance_matrix, dtype=float)


class Plot():
    def __init__(self): 
        self.cmap = plt.get_cmap('viridis')

    def _transform(self, X, dim):
        covariance = calculate_covariance_matrix(X)
        eigenvalues, eigenvectors = np.linalg.eig(covariance)
        # Sort eigenvalues and eigenvector by largest eigenvalues
        idx = eigenvalues.argsort()[::-1]
        eigenvalues = eigenvalues[idx][:dim]
        eigenvectors = np.atleast_1d(eigenvectors[:, idx])[:, :dim]
        # Project the data onto principal components
        X_transformed = X.dot(eigenvectors)

        return X_transformed

    def plot_regression(self, lines, title, axis_labels=None, mse=None, scatter=None, legend={"type": "lines", "loc": "lower right"}):
    
        if scatter:
            scatter_plots = scatter_labels = []
            for s in scatter:
                scatter_plots += [plt.scatter(s["x"], s["y"], color=s["color"], s=s["size"])]
                scatter_labels += [s["label"]]
            scatter_plots = tuple(scatter_plots)
            scatter_labels = tuple(scatter_labels)

        for l in lines:
            li = plt.plot(l["x"], l["y"], color=s["color"], linewidth=l["width"], label=l["label"])

        if mse:
            plt.suptitle(title)
            plt.title("MSE: %.2f" % mse, fontsize=10)
        else:
            plt.title(title)

        if axis_labels:
            plt.xlabel(axis_labels["x"])
            plt.ylabel(axis_labels["y"])

        if legend["type"] == "lines":
            plt.legend(loc="lower_left")
        elif legend["type"] == "scatter" and scatter:
            plt.legend(scatter_plots, scatter_labels, loc=legend["loc"])

        plt.show()

    # Plot the dataset X and the corresponding labels y in 2D using PCA.
    def plot_in_2d(self, X, y=None, title=None, accuracy=None, legend_labels=None):
        X_transformed = self._transform(X, dim=2)
        x1 = X_transformed[:, 0]
        x2 = X_transformed[:, 1]
        class_distr = []

        y = np.array(y).astype(int)

        colors = [self.cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]

        # Plot the different class distributions
        for i, l in enumerate(np.unique(y)):
            _x1 = x1[y == l]
            _x2 = x2[y == l]
            _y = y[y == l]
            class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))

        # Plot legend
        if not legend_labels is None: 
            plt.legend(class_distr, legend_labels, loc=1)

        # Plot title
        if title:
            if accuracy:
                perc = 100 * accuracy
                plt.suptitle(title)
                plt.title("Accuracy: %.1f%%" % perc, fontsize=10)
            else:
                plt.title(title)

        # Axis labels
        plt.xlabel('class 1')
        plt.ylabel('class 2')

        plt.show()